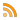Herzfunktion 2D

Ein Herz ist ein sehr beliebtes Designelement. Irgendwie scheinen Menschen darauf abzufahren, wenn sie ein Herz sehen. Es ist das eine große Symbol für Liebe und Freundschaft. So stellte sich mir als Designer die Frage: Wie kann ich das Herz mit der Mathematik verbinden?

Die Antwort war ganz einfach: mit einer Herzfunktion. Oder Herzkurve. Ich suchte eine Gleichung, die im x-y-Koordinatensystem eine Kurve in der Form eines Herzens beschreibt. Auf der Website mathematische-basteleien.de werden gleich mehrere Möglichkeiten aufgeführt, mathematisch ein Herz darzustellen. Ich habe mich für die folgende Form entschieden:

(x2 + y2 - 1)3 - x2y3  =  0

Das Ergebnis kann sich sehen lassen, ein wohlgeformtes Herz. Doch wie kommt es zustande? Was hat diese Formel zu bedeuten? Wie funktioniert sie?

Um diese Frage zu beantworten, möchte ich weiter ausholen. Ich versuche Schritt für Schritt zu erläutern, wie dieses Herz aufgebaut ist. Am Ende wird die o.g. Formel stehen, doch alles beginnt mit einem simplen Kreis.

Der Einheitskreis

x2 + y2  =  1

Dies ist die Gleichung für den Einheitskreis, d.h. den Kreis um den Koordinatenursprung herum und mit dem Radius 1. Wie ist diese Gleichung zu verstehen? Jeder Punkt (x|y) der x-y-Ebene, für den diese Gleichung gilt, ist Teil, des Einheitskreises. Jeder Punkt, für den sie nicht gilt, ist kein Teil des Einheitskreises. Dass das so ist, folgt direkt aus dem Satz des Pythagoras:

a2 + b2  =  c2

Diese Gleichung gilt in jedem rechtwinkligen Dreieck mit den Seitenlängen a, b und c, wobei c dem rechten Winkel gegenüberliegt. Unendlich viele solche Dreiecke lassen sich in den Einheitskreis einfügen (s. Bild). Die Seite c entspricht dabei immer dem Kreisradius (also c=1). a und b sind nicht nur die beiden anderen Seitenlängen des Dreieckes, sondern stellen ebenso die Koordinaten des Punktes dar, an dem das Dreieck den Einheitskreis berührt. Für jeden Punkt auf dem Einheitskreis gilt also:

x2 + y2  =  a2 + b2  =  c2  =  12  =  1

oder einfach:

x2 + y2  =  1

Wunderbar, der Einheitskreis also. Ein Kreis ist aber längst noch kein Herz. Die bisherige Kurve muss jetzt möglichst zielgerichtet verformt werden. Für diesen Zweck stelle ich die Kreisgleichung zunächst einmal um zu:

x2 + y2 - 1  =  0

und ersetze die Null durch einen allgemeinen Wert v:

x2 + y2 - 1  =  v

Für jeden Punkt der Ebene ergibt sich aus dieser Gleichung ein Wert v, in Abhängigkeit der Koordinaten x und y. Ist v=0, liegt der betreffende Punkt genau auf der Kurve, wie ich oben schon erwähnt habe. Innerhalb der Kurve dagegen ist dieser Wert stets kleiner als Null (z.B. -1 für für x=y=0), außerhalb größer als Null (z.B. +1 für x=y=1).

Verformen können wir die Kurve nun z.B., indem wir links einen festen Summanden d ergänzen:

x2 + y2 - 1 + d  =  v

Für positive Werte von d wird sich die Kurve zusammenziehen (kleinerer Radius), für negative Werte ausdehnen (größerer Radius).

Warum ist das so? Anschaulich gesagt: Für ein positives d wird für alle Punkte (x|y) auf der Ebene das resultierende v um den gleichen Wert d steigen. Punkte, bei denen das v vorher so gerade eben kleiner war als Null (knapp innerhalb des Einheitskreises), liegen anschließend im positiven Bereich (außerhalb des Einheitskreises). Die Punkte, für die v=0 wird, liegen weiter innen als bisher (weil bei ihnen x² + y² kleiner wird, was das positive d ausgleicht) – die Kurve zieht sich zusammen. Ist d negativ, muss es durch höhere x- und y-Werte ausgeglichen werden. Die Kurve für v=0 liegt also weiter außerhalb – sie dehnt sich aus. Bei all dem bleibt es aber leider bei einem simplen Kreis.

Um ein Herz zu erreichen, müssen wir die Kurve zwar schrumpfen und dehnen, aber nicht gleichmäßig und nicht in jedem der vier Quadranten auf dieselbe Weise.

Herz aus Ellipse

Zunächst nehmen wir uns vor, die bisherigen Schnittpunkte des Einheitskreises mit den Koordinatenachsen zu erhalten. An den Punkten (+1|+1), (-1|+1), (+1|-1) und (-1|-1) soll die linke Gleichungsseite, also das resultierende v, unbeeiflusst bleiben. Das können wir erreichen, indem wir das konstante d ersetzen durch d(x,y) = x⋅y. Für x=0 oder y=0, also auf den Koordinatenachsen, gilt stets d(x,y) = 0, was seinen Einfluss eliminiert – ganz wie wir es wollten. Wir erhalten (indem wir auch das v wieder durch Null ersetzen):

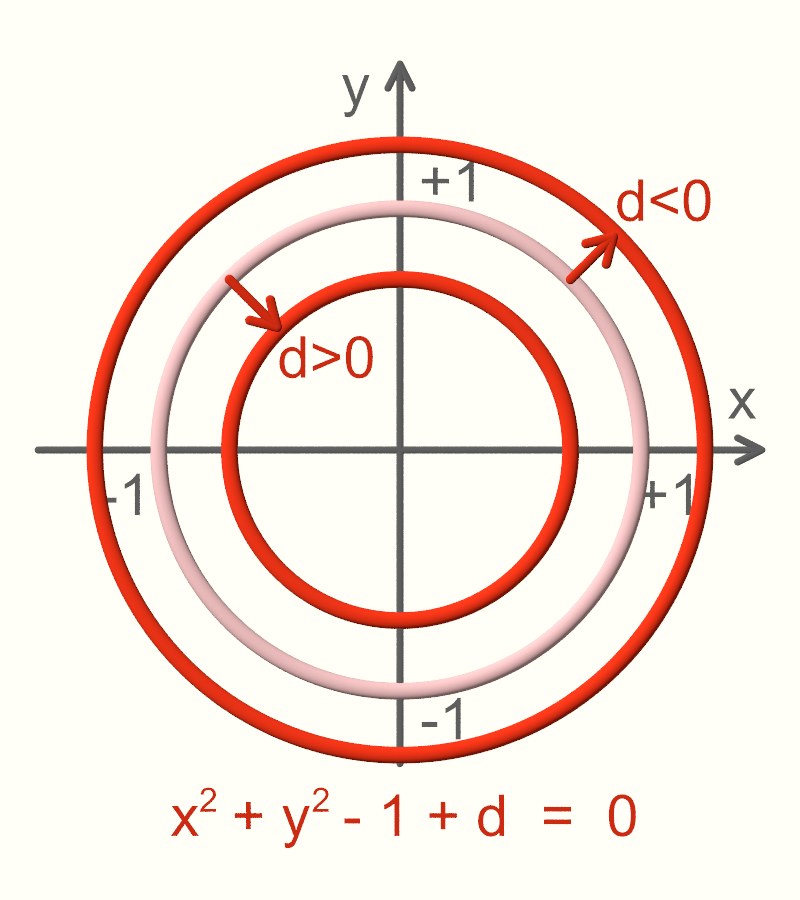
x2 + y2 - 1 + x⋅y  =  0

Das Ergebnis ist eine Ellipse, die die Koordinatenachsen an denselben Punkten schneidet wie der Einheitskreis. Und siehe da: Die linke Seite dieses Bildes zeigt schon die typische Herzform. Die rechte auch, nur steht sie hier auf dem Kopf.

Bevor wir das korrigieren, betrachten wir die beiden linken Quadranten einmal genauer. Oben links, also für x<0, y>0, wird die Kurve nach außen gedehnt. Klar, denn d(x,y) wird hier immer einen negativen Wert annehmen (da x negativ und y positiv ist). Dies verringert den Gesamtwert der linken Gleichungsseite für alle Punkte (x,y) in diesem Quadranten mehr oder weniger stark. Zu den Koordinatenachsen hin wird dieser Einfluss allerdings immer schwächer und verschwindet auf den Achsen ganz. Es ensteht eine Beule. Im linken unteren Quadranten, also für x<0, y<0, verbiegt sich die Kurve nach innen, zum Ursprung hin, da d(x,y) hier immer positiv ist (x und y sind negativ; Minus mal Minus ergibt Plus).

Jetzt spiegeln wir zunächst die linke Seite an der x-Achse, indem wir x durch den Betrag von x ersetzen, also das Vorzeichen eliminieren (d(x,y) = |x|⋅y). In der linken Bildhälfte wechselt d(x,y) dadurch das Vorzeichen; wo es vorher positiv war, wird es negativ und umgekehrt. Die Einflüsse im oberen und unteren Quadranten kehren sich dadurch genau um. Man könnte auch sagen: Das |x| lässt die Gleichung glauben, sie wäre rechts, wenn sie eigentlich links ist. Wir erhalten:

x2 + y2 - 1 + |x|⋅y  =  0

Unsere Ergänzung d(x,y) ist in dieser Gleichung auf der gesamten oberen Ebenenhälfte positiv, unten dagegen negativ. Wenn wir nun das Vorzeichen genau umkehren (d(x,y) = -|x|⋅y), dann spiegeln wir das gesamte kopfstehende Herz noch einmal an der x-Achse:

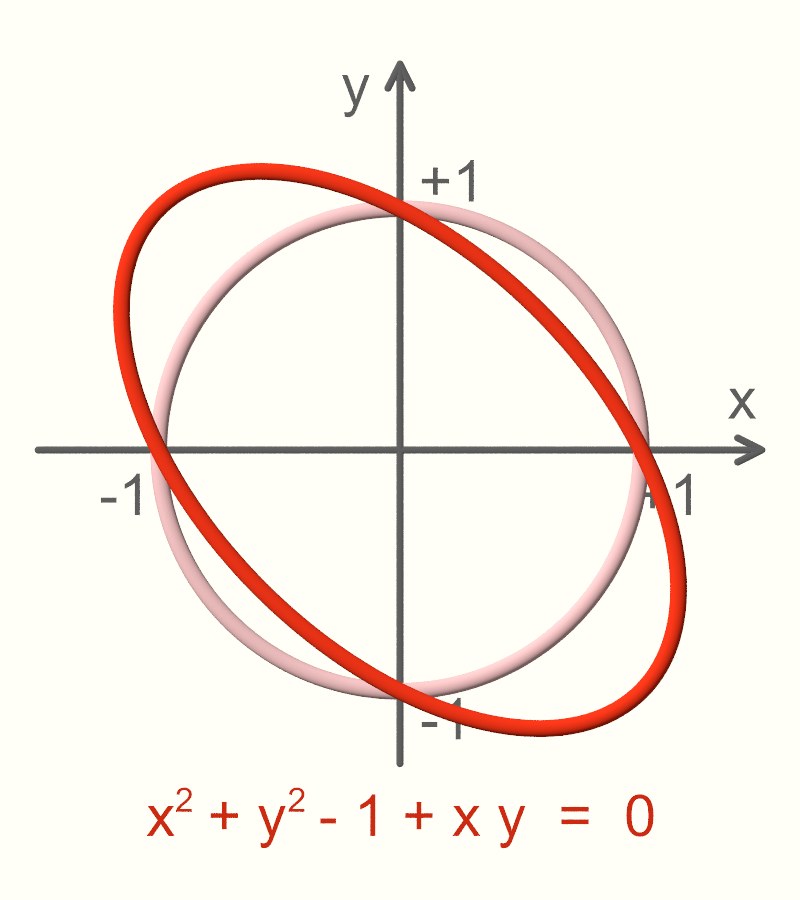
x2 + y2 - 1 - |x|⋅y  =  0

Als Ergebnis erhalten wir ein schönes Herz, entstanden aus einer Ellipse. Ob es weniger schön ist als das Herz ganz oben, darüber kann man streiten. Mir jedenfalls fehlt noch der kleine Schwung an der Spitze.

Herz mit Schwung an der Spitze

An dieser Stelle verlasse ich den Pfad des zielgerichteten Verformens. Stattdessen spiele ich ein wenig mit der Funktion herum und bemerke, dass die Spitze sich verschönert, wenn ich |x| mit einem Wert kleiner als Eins potenziere, z.B. mit 2/3:

x2 + y2 - 1 - |x|2/3⋅y  =  0

So habe ich mir das Ergebnis vorgestellt. Dieses Herz ist nicht nur schön, sondern auch elegant und sanft geschwungen. Es hat den erwünschten leichten Schwung an der Spitze, und die beiden Bögen ganz oben sind noch etwas höher gezogen, ohne dass das Herz breiter wird. Diese Version entspricht exakt meinem Wunschergebnis ganz oben auf dieser Seite. Und doch ist es eine andere Gleichung. Beide können aber leicht ineinander umgeformt werden, indem die gesamte Gleichung geschickt umgestellt und mit 3 potenziert wird. Dabei kann auf die Betragsstriche verzichtet werden, da das x den Exponenten 2 erhält, der ebenfalls das Vorzeichen eliminiert:

x2 + y2 - 1 - |x|2/3⋅y  =  0
<=>  x2 + y2 - 1  =  |x|2/3⋅y
<=>  (x2 + y2 - 1)3  =  |x|2⋅y3
<=>  (x2 + y2 - 1)3  =  x2⋅y3
<=>  (x2 + y2 - 1)3 - x2⋅y3  =  0

Damit bin ich fertig.

Letzte Variationen

Selbstverständlich kann ich auch mit dieser Gleichung noch herumspielen. Mit einem konstanten Faktor kann ich den Einfluss von d(x,y) verstärken oder abschwächen, je nach Geschmack. Hier ein paar Beispiele:

Ich entscheide mich aber für die Version ganz oben (konstanter Faktor gleich 1). Mit dieser Gleichung kann ich mathematisch exakt ein Herz beschreiben. Ich kann es in Grafikprogramme oder Funktionsplotter eingeben und voilà – ein Herz.

Klar, dass ich eine Reihe von Motiven in meinem Shop habe, die dieses Herz verwenden :-)